

You can download further information about Similar triangles. If the ratio of the hypotenuse and one side of a right-angled triangle is equal to the ratio of the hypotenuse and one side of another right-angled triangle, then the two triangles are similar. If each of the sides of one triangle can be matched up with each of the sides of another so that the ratios of matching sides are equal, then the two triangles are similar. 03 Similarity in Right Triangles Right Triangle Similarity Theorem. If the ratio of the lengths of two sides of one triangle is equal to the ratio of the lengths of two sides of another triangle, and the included angles are equal, then the two triangles are similar. View 8-3-Similarity in Right Triangles Key.pdf from MATH 2303 at University of Houston. We use these similarity criteria when we do not have the measure of all the sides of the triangle or measure of all the angles of the triangle. Understand similarity in terms of similarity transformations (G.SRT.1-3).

Right triangle similarity pdf#
pptx), PDF File (.pdf), Text File (.txt) or view presentation slides.
Right triangle similarity free#
Re-stating this fact is not required when using the AAA test in a similarity proof. Similarity, Right Triangle Trigonometry, and Proof. Right Triangle Similarity Theorem - Free download as Powerpoint Presentation (.ppt /. Because the angle sum of a triangle is always 180°, the third pair of angles will automatically be equal. Geometry B, Quiz 2: Similarity: Triangle Theorems. Since WZX and WXY are similar, the ratios of corresponding sides. It is sufficient to prove that only two pairs of angles are respectively equal to each other. Right Triangle Similarity Quiz QuizletRight Triangle Similarity Assignment. So, WZX and WXY are similar by the AA Similarity Theorem. ay bx (1) y (2) (2) 1 y 4 divide both sides by 1, in order to eliminate the 1 from the problem. If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar. The outcome should be similar to this: a y b x Now, say that we knew the following: a1 b2 x2 We wished to find the value of y.
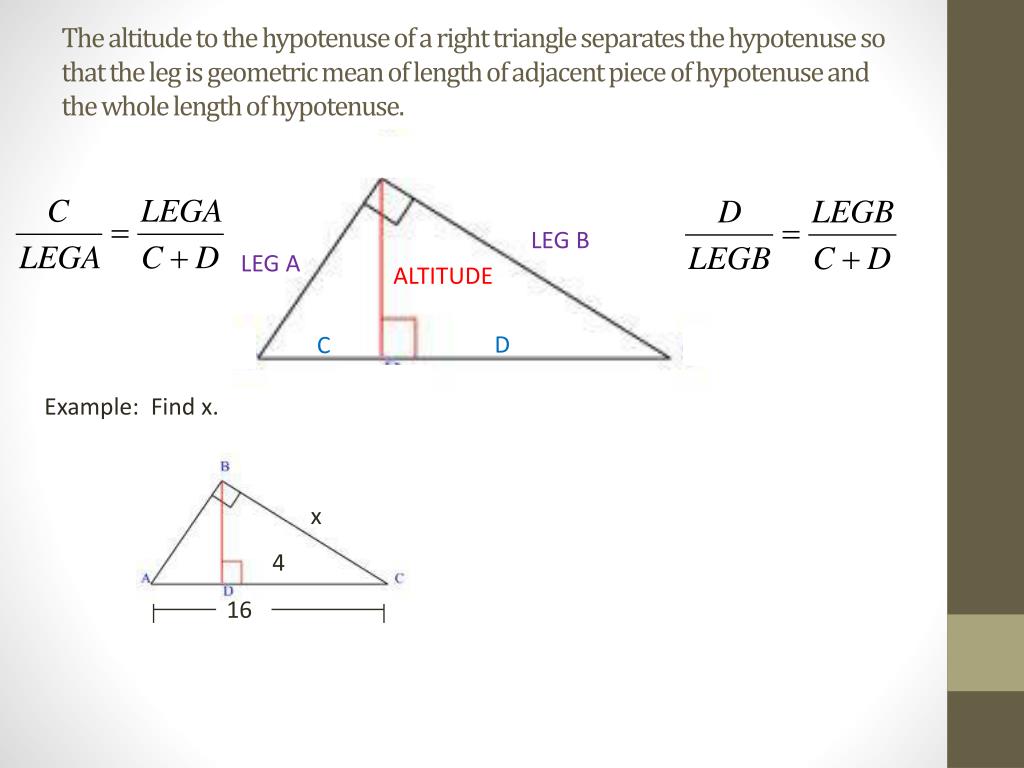
Side-Side-Side Similarity (SSS) Theorem: If the corresponding sides of two triangles are proportional, then the triangles are similar. There are four similarity tests for triangles. Side-Angle-Side Similarity (SAS) Theorem: If an angle of one triangle is congruent to an angle of a second triangle, and the sides that include the two angles are proportional, then the triangles are similar. This proves the triangle angle bisector theorem: the angle bisector of one angle of a triangle divides the opposite side of the triangle into segments proportional to the lengths of the other two sides of the triangle.It is helpful if students are also familiar with the tests for congruence.


 0 kommentar(er)
0 kommentar(er)
